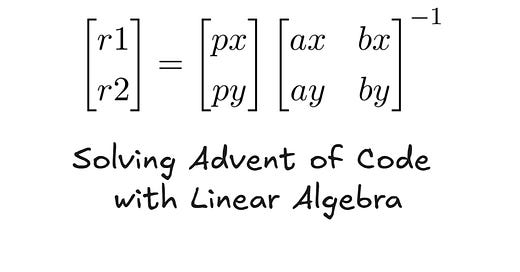Linear algebra pops up in Advent of Code 2024

As soon as I figured out that the problem statement is just to solve a system of 2 linear equations, I thought this would be a chance to put that college degree to use and learn some numpy!

Cover image showing Solving Advent of Code with Linear Algebra and numpy in Python

If you’re not yet familiar with Advent of Code, it is a website where each year (since 2016) the creator Eric Wastl, posts programming contest puzzles with a fun story from Dec 1st to 25th much like in an advent calendar fashion. Well, this year was no different and I convinced a few friends to also try the same out and they seem hooked. Apart from being a contest, it has a lovely story and aims to teach some new thing/concept through each puzzle and apply your knowledge to the puzzle at hand. So far I’ve came across a bit where my previous knowledge was helpful and i could modify/use standard techniques at the problem.

---

Coming to Day 13 of the challenge, where the data given is like this:

Button A: X+94, Y+34
Button B: X+22, Y+67
Prize: X=8400, Y=5400

We are asked to find after how many presses of button A and button B will we reach the prize?

Go on think for a while about how you would approach it.

---

After thinking a bit as to how to approach this, it dawned that we have to find a combination that after lets say a presses of button A and b presses of button B, we can get there in general. This will help to formulate the problem statement in the following fashion into two linear equations.

\(94a + 22b = 8400 \)

\(34a + 67b = 5400\)

Now we just have to find solutions to the equation aka, solve for a and b.

Suppose we take the first two coefficients from Button A (here, 94 and 34), as ax and ay respectively, and similarly pull out bx and by from the Button B (here, 22 and 67). We take the prize’s x and y coordinates as px and py respectively.

a, b, prize = m.split("\n")
ax, ay = [
    int(a.split(",")[0].split()[-1].replace("X+", "")),
    int(a.split(",")[1].replace(" Y+", "")),
]
bx, by = [
    int(b.split(",")[0].split()[-1].replace("X+", "")),
    int(b.split(",")[1].replace(" Y+", "")),
]
px, py = [
    int(prize.split(",")[0].split()[-1].replace("X=", "")),
    int(prize.split(",")[1].replace(" Y=", "")),
]

We can now represent the coefficients in a matrix using numpy which will be analogous to this representation:-

\(\begin{bmatrix} ax & bx \\ ay & by \end{bmatrix}\)

M = np.array([[ax, bx], [ay, by]])

Similarly we can represent the prices as:-

\(\begin{bmatrix} px \\ py \end{bmatrix}\)

R = np.array([px, py])

This will allow us to solve for the equation in the following formulation as matrix multiplications, where r1 and r2 are the actual solutions to the problem of linear equations with the given coefficient matrix.

\(\begin{bmatrix} ax & bx \\ ay & by \end{bmatrix} \begin{bmatrix} r1 \\ r2 \end{bmatrix} = \begin{bmatrix} px \\ py \end{bmatrix}\)

We can compute the inverse if the coefficient matrix is not singular, i.e. the determinant is not zero, and then multiply it to get the result. The next step will hence look like,

\(\begin{bmatrix} r1 \\ r2 \end{bmatrix} = \begin{bmatrix} px \\ py \end{bmatrix} \begin{bmatrix} ax & bx \\ ay & by \end{bmatrix}^{-1}\)

This same operation is taken care of by numpy for us in the numpy.linalg module. It exposes a solve function that can take in our coefficient matrix and result matrix and then give the result matrix, i.e. r1 and r2

soln = np.linalg.solve(M, R)

There are a few modifications to be made that are the constraints of the current AoC ( Advent of Code) problem.

The solution must be in whole integers, since we cannot push a button for a fractional amount. The solution would then need to rounded off.

So we can use the rint function that will round our array elements to integers.

 soln = np.rint(np.linalg.solve(M, R))

This will solve the problem, but now we might have introduced some issues. You see, the fractional values will work absolutely for the equations. But after rounding off, if the values were not integral to begin with, they will get altered and thata does not satisfy the problem anymore. We thus can implement a cross check to verify that it still satisfies our R matrix.

if np.all(M @ soln == R):
    p1 += cost(*soln) # this is just 3a+b from the solution

Two things to unpack here, the special @ is provided/overloaded by numpy to perform matrix multiplications seamlessly, and hence we can quickly do another matrix multiplication according to our original formulation to see if the inverse is actually satisfying the prize after rounding off. If they are, we can add it as part of the solution.

For adding to the solution, we are told to calculate the cost which is just 3 times the button A and 1 times the button B that we push and as many tokens are spent.

We repeat the above for each machine in the input. Calculate the solutions using matrix inverse, round the values, cross-check to see if that still satisfies, and then add to the running total.

That gives us the answer to part 1 of the puzzle.

Now onto part 2.

Sometimes the part 2 can be very difficult to solve if the original solution to the problem was not modelled correctly and we could have to start over, or maybe find another way. We are expeced to modify our solution slightly so as that it solves both parts. It is like the customer changing requirements in future that will have to be accounted for in the system now.

In this case, we are told that the actual prizes are off by 10000000000000 and thus the real values for the example above is X=10000000008400, Y=10000000005400.

What do we do now to account for this change?

Thankfully, we already have the system in place! We just need to offset our r1 and r2 values to account for that correction and let our solution run as before.

CORRECTION = 10000000000000
R2 = np.array([px + CORRECTION, py + CORRECTION])

soln2 = np.rint(np.linalg.solve(M, R2))

if np.all(M @ soln2 == R2):
    p2 += cost(*soln2)

That will be the end of day 13! I hope you found this useful and maybe got to learn something new. I got to know about the solver in numpy and gained exposure and a place to practically implement the courses I took . This largely helped in my journey with learning Python and also solving problems for interview prep and the like.

---